Vitamin D: Harvesting the Diversification Premium Through Prudent Leverage

We begin our discussion with a story to help us think about risk and bet sizing. Our protagonist, poker aficionado Annie, enters a casino prepared for a night of risk and reward. As a competent player, she finds she walks away with a few extra dollars in her wallet at the end of the night more often than not. However, her success varies based on both the skill of her opponents as well as pure, blind chance. She knows that if she plays at a table where she is more skilled than most at the table, she will win money in the long run. And if she is the least skilled player… Well, at least she has fun while losing.

Being a process-oriented woman, Annie likes to manage the risk of choosing a dangerous table where she might be outmatched by balancing her time between different poker tables. She usually moves on to a new table after an hour or so, rotating throughout the night. By doing so, she distributes her risk by competing with many different players, rather than concentrating on a single potentially losing table.

On this particular night, there are two tables with open seats that Annie could join. One is a high stakes table with large bets; hundreds of dollars are at stake every hand. The second is a low stakes table with smaller bets, averaging around $20. Annie has no way of determining the skill of the players at either table and therefore any potential advantage she may have, so she decides to follow her policy of balancing risk.

Imagine that Annie decides, naively, to simply allocate her time evenly between the two tables. Or perhaps, a 60/40 split between the high stakes and low stakes tables, given she would like to make enough money to go on a nice Caribbean vacation (post-COVID). As you can imagine, since each hand is many times larger at the high stakes table, Annie’s earnings will be almost entirely determined by the high stakes table, despite her efforts to divide her risk. The volatility of that table is higher, and in the short run, a few unlucky hands could eliminate an entire productive night at the low stakes table.

Instead, Annie takes the more reasonable course of action to divide her time proportional to the bet size (risk) of the table. This means she spends more time at the low-risk table and plays relatively briefly at the high stakes table. By doing so, she manages to achieve a more balanced risk profile between the two tables, each contributing equally to the thickness of her wallet at the end of the night.

So, how does the world of poker relate back to the world of finance? We can think of the high stakes table as “equities” and the low stakes table as “bonds.” Equities have larger moves when compared to bonds, which we can think of as larger bet sizes. Where Annie allocates time, we allocate capital. We will see how thinking about poker tables and balancing risk can help us to understand the Risk Parity investment strategy and create more balanced, well-rounded portfolios.

Suppose that Annie has a goal of making $500 in a night. However, playing at the low stakes table makes that goal difficult. We can imagine she might want to raise the average bet size at the low stakes table so that it has the same risk as the high stakes table. While our friend Annie has limited options, we will see that in financial markets, we can use responsible leverage to raise the bet size of the low stakes table, without changing any of its other properties, such as who we’re playing with or our probability of winning hands.

As financial market participants, we are used to dealing with the uncertain nature of potential investment outcomes – not unlike the uncertain outcomes of a poker game amongst skilled players. Investors provide money to entities like governments, corporations, and individuals, hoping to generate a sufficient return on their capital that justifies the perceived “risk” from providing that capital. In order to part with their hard-earned capital, investors must be compensated for considerations like, for example, having to delay the purchase of their new summer home. In addition, if something unexpected occurs and the investment goes sideways, the summer home might then become unattainable.

But, what do we really mean by “risk”? To help us understand the definition of “risk,” we need to realize that while similar, there are nuanced differences between “risk” and “uncertainty.” Risk is understanding and managing the odds of various outcomes with certainty. Uncertainty is realizing that all potential outcomes are not known beforehand. When we draw a playing card from a fair deck, we know with certainty that there is a 25% chance of drawing a face card. Betting on whether you will draw a face card is true “risk.” Uncertainty is expecting there to be a 25% chance of drawing a face card, and instead drawing a purple two of clubs. Uncertainty is when the rules of a game are either unknown or fluid and change regularly, causing data points to not conform to a predictable distribution.

At the poker table, you can manage the risk of drawing poor cards. However, if a new player joins the table, the game changes as uncertainty about their playing style is introduced and our risks change. What used to be a winning position could swiftly turn into a losing game. The game never remains constant, just like in finance.

The risk of drawing a purple two from a deck of cards is commonly referred to as the “Black Swan” problem, made popular by Nassim Nicholas Taleb. Drawing on the work of philosopher David Hume and the shortfalls of inductive reasoning, Taleb uses the theory to explain why the probability of rare events cannot be computed beforehand. While the COVID-19 pandemic was not a pure “Black Swan” in the traditional sense (more of what Donald Rumsfeld would classify as a known-unknown), it highlights the difference between risk and uncertainty. In November of 2019, the possibility of a novel virus delivering a staggering blow to financial markets was not on anyone’s radar, thus few were focused on managing this sort of risk. The subsequent increase in volatility (risk knowable after the fact) is inherently linked to the amount of uncertainty investors are feeling about the future. The main distinction here is that for investors, risk is only knowable after the fact, and because all potential outcomes in the future can’t be modeled with accuracy, the future becomes shrouded in uncertainty. The purpose of this rather long-winded preamble is to introduce the concept of a Risk Parity investment strategy, which incorporates the concepts of both risk and uncertainty into its portfolio construction methodology.

The Risk Parity portfolio was popularized by Ray Dalio at Bridgewater in the late 1990s, with the creation of the “All Weather” portfolio. There are numerous ways an investment manager can construct a Risk Parity framework, but the high-level concept is that the asset classes within an investor’s opportunity set each contribute the same amount of risk (historical) to the overall portfolio. Hence, the asset allocation is balanced by risk, not dollars. The Risk Parity framework observes the historical risk and correlations of asset classes in an investment universe. We then employ well understood techniques to ensure that the portfolio’s potential gains and losses are evenly distributed across our investments. Philosophically, Risk Parity embraces the uncertainty of the future. We make no claims about which assets we think will perform best, instead choosing to balance our bets across a range of assets that perform well or poorly in different market environments.

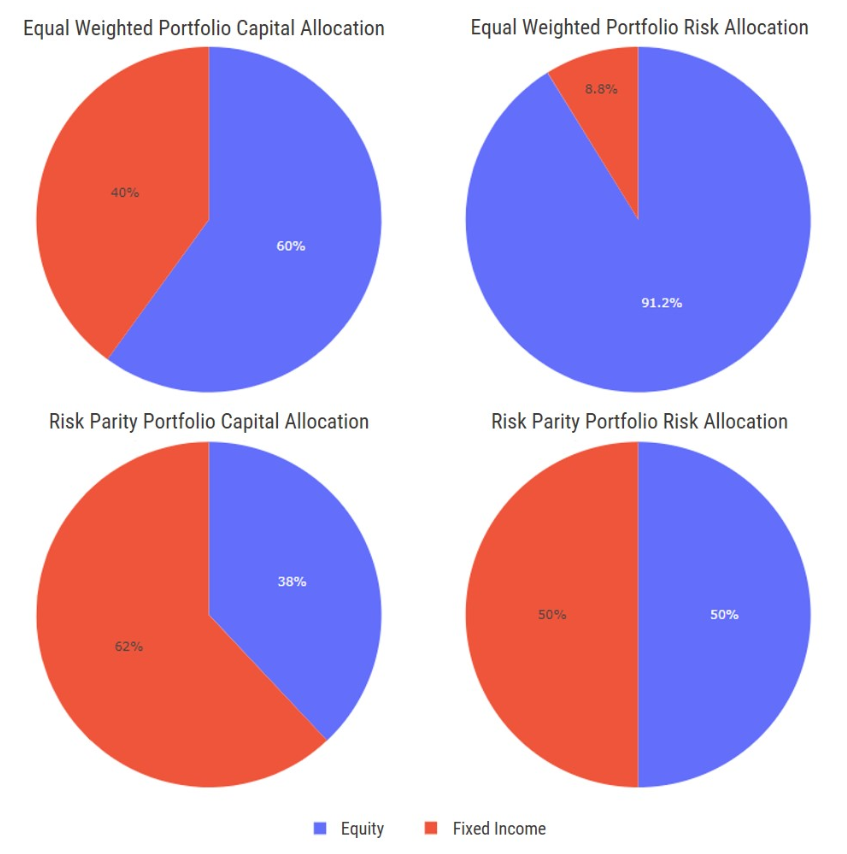
This is different than traditional portfolio construction where a dollar allocation to specific asset classes occurs based on an investor’s required return and risk objectives. The challenge with the traditional framework is that in a global balanced portfolio (60% equity and 40% fixed income), the majority of the portfolio’s risk (realized volatility) is determined by the allocation to equities, much like our poker player realizing that the volatility of her earning potential is denominated by her play at the high stakes table.

By balancing asset allocation by risk and not dollars, the composition of a Risk Parity portfolio relative to a traditional balanced portfolio varies quite substantially. With an expanded opportunity set that includes commodities and real return bonds, the Risk Parity portfolio tends to place more weight in low-risk assets (e.g., fixed income), as well as assets that add to overall portfolio diversification (e.g., commodities) while reducing the allocation to equities.

The result of creating a portfolio where the underlying asset classes contribute the same amount of risk to the portfolio results in a much more efficient portfolio as defined by return per unit of risk, known in finance as the Sharpe Ratio. This can be seen in the graph below, which compares the Risk Parity portfolio to other asset classes based on returns (y-axis) and risk (x-axis). We plot a few thousand diversified portfolios constructed by using different combinations of each asset class. You can see a distinct bullet shape in the chart, known as the “Efficient Frontier,” which represents the best possible bang for your buck that you can achieve by holding some fixed combination of the asset opportunity set.

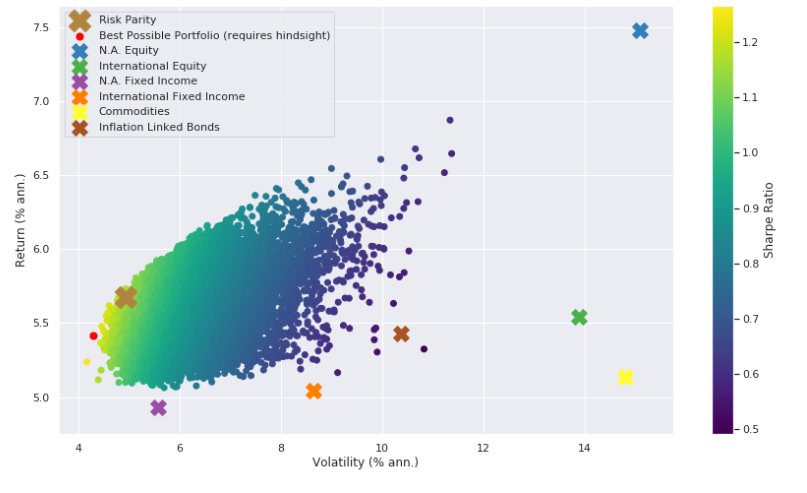
Now, as you may have noticed, the Risk Parity portfolio (bold gold x) is dubbed “more efficient” than an equity-centric portfolio (blue x) given the expected return per unit of risk based on empirical data is higher. However, who cares about “a more efficient portfolio” if the returns are lower than just holding equities! Even if the return per unit of risk is superior to other portfolios, for the investor who needs to achieve a 7% return target to fund their investment objectives, this portfolio falls short. Typically, what would happen in this situation is that in order to achieve the higher return target, the investor would increase their exposure to equities, an asset class with a higher expected return. While this increases both the uncertainty and risk of the portfolio, the investor needs to hit their return target and is thus forced into adjusting their asset allocations away from the optimal portfolio. We would argue that the more efficient way to achieve a desired return objective is by taking a superior portfolio and adding a prudent amount of leverage in order to increase the expected return.

Using leverage to increase the expected return of the optimal portfolio is not a new idea. Instead, it is the bedrock of modern finance embedded in what is known as the capital allocation line.

We are not advocating that leverage doesn’t come with risks. We just believe that using a judicious amount of leverage on an extremely efficient portfolio is a better risk to take than placing a higher concentration of dollars in a higher beta asset class (e.g., equities) to achieve the desired return target. In fact, leverage can be managed appropriately in a variety of different ways, while the concentration strategy is more akin to what one could call “hope and pray.” The below graph shows that when a static leverage multiple is used to increase the expected volatility of the Risk Parity strategy to one similar to global equity markets, we are able to scale the Risk Parity portfolio up to the same volatility (risk) as an equity portfolio by traversing along the dashed line. Recall that we defined the Sharpe Ratio as the return per unit of risk. By using a leverage constant, we can trade risk for additional return, scaling up to some predetermined risk level. This technique allows us to harvest the stylized “diversification premium,” which can result in achieving a much higher return for the same level of risk. A commonly cited aphorism made by stock pickers is that you can’t eat a Sharpe Ratio, since at the end of the day realized returns are what matter to investors. We show that with prudent leverage, you can’t just eat your Sharpe Ratio – you can feast on it to the tune of several percentage points a year.

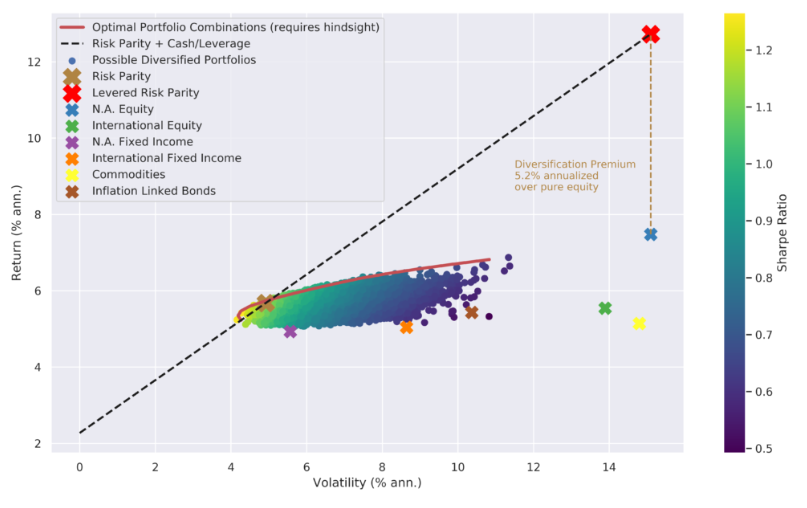
Now that we’ve shown how using a judicious amount of leverage in a Risk Parity strategy to match the risk parameters of global equity markets should provide a more efficient outcome for the end investor, we can pivot back to how the strategy relates to risk and uncertainty. Unlike other traditional active investment strategies where a manager will make a forecast on which asset classes will outperform and adjust their asset allocation accordingly, the Risk Parity strategy makes no such forecast on asset class returns.

Risk Parity is by no means a “tail-risk” or “Black Swan” protection strategy, merely it accepts uncertainty by diversifying portfolio “bets” across a wide variety of asset classes in order to more reliably harvest risk premia. The active component of the strategy is that once the model has determined the optimal portfolio construction needed to achieve equal risk contribution from each asset class, leverage is applied dynamically to the portfolio to target a certain volatility. The dynamic leverage model can be thought of as how the portfolio scales the size of its bets based on changes in ex-post volatility and covariance between the assets in the portfolio.

For example, as volatility in financial markets increases, the range of expected outcomes increases as a result. By reducing leverage as volatility increases, the strategy is able to react to the increases in the ex-ante uncertainty of future asset class returns. If an investor did nothing to adjust their asset allocation when volatility spikes, this is akin to naively increasing your “bet” on the expectation of future returns for that asset class. If you were allocating 60% of your portfolio to global equities when rolling one-year volatility was at 10%, your naive return expectations have to increase in order to justify your similar asset allocation if volatility spikes to 20% on a rolling basis. In other words, imagine you were willing to risk $10 for the proposition of making $20. Then, the risk (volatility) doubles and now you need to put up $20 to make the same bet. Obviously, if you’ve doubled your risk, you should double your reward! The irony is that when volatility increases and investors are being asked to put more money down, it usually occurs during periods of uncertainty – the financial crisis, COVID-19, European debt crisis; usually the time most people want to de-risk, not double down!

As our Manager of Investment Research and Analytics, Amin Haji, recently wrote in his series of blog posts on volatility, as volatility increases, the mean and median for expected values diverge. Because the average investor does not get to experience the average return of an underlying investment strategy (a more conservative assumption is the median), an expanding volatility profile combined with a static asset allocation inherently increases your bet sizes. Therefore, by adjusting your leverage ratio based on a certain volatility target, the overall stability of the portfolio should be greater through numerous simulations of return paths than a traditional balanced portfolio where no volatility scaling is undertaken.

For Part II of this series, we will dive into the improved stability of a portfolio that dynamically adjusts leverage.