Wanna Bet? How Much?

What is the largest amount of money you would bet on a fair coin flip?

I like asking people this question, because the answers I get are often very interesting and very diverse. It gets at the heart of a person’s risk tolerance, as it is a bet with an expected value of 0, given that it’s a fair coin flip, but you can win or lose on any flip and for many flips. Some people will respond $0, whereas others will bet $5, $10, or even $100+. Since the bet has no expected value, this question is primarily psychological, although it can be shown that there is an optimal amount that you should bet on this coin flip. But, we’ll get to that a bit later.

First, let’s look at a biased coin. Let’s say the coin will come up heads with a probability of 55%. What is the largest amount of money you would bet now? Let’s assume you have an opponent with an infinite supply of money and that he will offer you this bet as many times as you want to take it. (Yeah, he’s rich – but he’s not very smart, is he?) Now the question becomes, how much should you bet?

Most people have some amount of money they are willing to invest. Every investment, unless it’s an arbitrage, is a gamble. It’s a bet. For this article, let’s call this investable money our bankroll. So, how much of our bankroll should we bet? It can be shown that if you want to maximize your expected gain, you should bet it all (1). There is a flaw with this, though, since it can also be shown that you have a 90% chance to lose it all after as little as three flips of our biased coin. There must be a better way.

In 1956, John Kelly published a paper introducing a concept now known as the Kelly Criterion. In this paper, he set out to find what fraction of our bankroll we should bet to maximize our bankroll growth. I will spare you the math, but the formula is both elegant and informative. If p is our probability of winning a bet, q is the probability of losing, and b are the odds we are being offered on our bet expressed as a fraction of what we will lose, then the percentage of our bankroll that we should bet is given by:

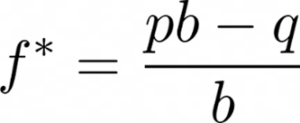
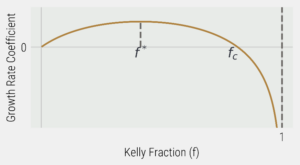
Since b is 1 in our example above, this simplifies to f* = p-q. In most cases, q=1-p since you either win or lose the bet; hence, the Kelly Criterion says you should size your wager proportionately to your edge. An attractive property of the Kelly Criterion is that you are always betting a fraction of your current bankroll, so if you lose, your next bet will be less, meaning you can never go bankrupt using this method. For the biased coin we have been discussing, we would maximize our bankroll growth by betting 10% (0.55-0.45) of our bankroll. We can see this in Figure 1 where we also show the f_c, which, if we bet a fraction of our bankroll larger than this amount, we will move into a negative growth rate even though our bet has a positive expected value.

What about if we were offered 5-4 on a fair coin flip? That would also be 10% of our bankroll as b = 5/4 = 1.25. These two scenarios seem equivalent since the Kelly fraction is identical. Still, with our 55% biased coin, we would expect to double our bankroll after 139 flips, whereas with a fair coin getting paid 1.25-1 on our money, we would expect to double our bankroll after 112 flips.

We can see from the above discussion that the Kelly Criterion shows that a rational bettor (investor) should not bet everything on a single investment. It is much better to have many small bets rather than a single large bet and this is directly analogous to an investment portfolio and diversification.

What about the original question of how much you should bet on a fair coin? Well, p=q and therefore f*=0, but that isn’t very fun, is it?

Note: Full Kelly betting is extremely aggressive and rarely used in practice, as your edges are rarely ever known and betting too much is punished more severely than betting too little and could cause you to lose all your capital. Fractional Kelly is preferred, as it produces decent growth with significantly less risk.

References:

1. Thorp, E., The Kelly Criterion In Blackjack, Sports Betting, and the Stock Market