Strategic Bluffs: Game Theory in Action

Strategic decision making involves the identification and evaluation of choices to determine the best course of action to achieve specific goals. In the early 19th century, John Von Neumann published On the Theory of Games of Strategy, which birthed the field of game theory. This theory has revolutionized our understanding of complex interactions in diverse fields, such as economics, politics, and biology, and it has applications for everyday choices as well. Building upon the work of Von Neumann, John Nash emerged as a brilliant mind and was immortalized in the Oscar-winning film, “A Beautiful Mind,” starring Russell Crowe. Nash introduced the concept of the Nash Equilibrium, which provided a profound insight into the outcomes of non-cooperative games where each player’s success is dependent on the strategies of others. In simple terms, the Nash Equilibrium describes a situation in which no player can benefit by changing their strategy while the other players keep their strategies unchanged. Today, I would like to explore this using two simple games.

Let’s imagine you are competing in the high-stakes world of office Roshambo (rock, paper, scissors), and you are about to play me – the reigning, undefeated champion of Roshambo. Your palms are sweaty, you’re nervous. You know that every time you throw rock, I am already on paper. You switch to scissors, and BAM! I hit you with rock. I’m living in your head rent-free. What do you do? Do you wave the white flag of surrender and accept a fate of Roshambo inferiority? No, you study up on game theory and build an optimal unexploitable strategy and…*drumroll, please*…you randomize your choices so that you play rock, paper, scissors equally {1/3, 1/3, 1/3}.

This is the Nash Equilibrium for Roshambo, and playing this way makes you unbeatable. Unfortunately, it also means you can never really win. How does this work? Well, let’s imagine that you deviate slightly from this strategy and begin to play scissors slightly more often in an attempt to exploit my preference for paper. Then, I can immediately switch to a pure rock strategy and crush your pesky scissors. Any small deviation from optimal results in an exploitive pure adjustment by our opponent, but we can also see that if you deviate and I continue to play the optimal strategy, it has no effect. No player can benefit by changing their strategy. I have been defeated by math, and I am forever saddened. But this isn’t just about Roshambo. Let’s pivot to a more complex yet intriguing application of game theory: the AKQ game. The following discussion will heavily lean upon work by Bill Chen and Jerrod Ankenman in their book The Mathematics of Poker.

The AKQ game, a simplified poker variant, uses a three-card deck, containing an Ace, a King, and a Queen. In this game, an Ace beats a King, which beats a Queen. We are going to keep it very simple and force the first player (Alice) to check (pass), and then give the second player (Bob) the option to bet or check. If the second player bets, then the first player now has a decision to either call or fold. Before the betting begins, each player must put an ante of $1 into the pot, and only a Stratbet size of $1 will be permitted. Before we go any further, it is interesting to think about what your strategy for this game would be as Bob or as Alice. Take a moment to think about it.

Obviously, Bob will have to bet if he has an Ace, and maybe Bob is very conservative and decides that he will only bet when he has an Ace. Alice is smart, so Alice always folds whenever Bob bets, and Bob begins to get upset, because he isn’t getting enough value from his Aces. He is being exploited by Alice. Bob is going to have to do something else if he expects Alice to call him, but what should he do? Should he bet a King? Should he bet a Queen? How often should he bet? Game theory can help us answer these questions and provide an exact answer as to what Bob should do.

To develop a full strategy, we need to look at all options for all players for all possible cards, which is why we are studying the simplified half-street version of this game, as it is tractable. The full game tree is shown in Figure 1, where Bob’s actions are in Blue and Alice’s are in green. Let’s see if we can simplify the game by evaluating each of the options logically.

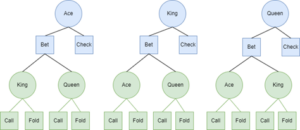
First, we can look at the options for Alice. If Bob checks behind after Alice checks, then Alice has no more decisions, because the game is over. So, we only care about Alice’s options after Bob bets. If Alice holds an Ace, she will always call as she holds the “nuts” – the best possible hand – and will win. In the parlance of game theory, we would say that calling with an Ace “dominates” folding an Ace. What about when Alice holds a Queen? Well, in this case, she has the worst possible hand, and she would always fold as she can never win, so folding dominates calling. We have reduced Alice’s decisions down to what she is going to do with a King and this can be seen in Figure 2.

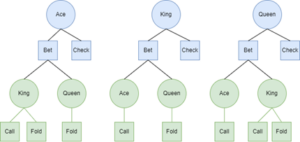
Now, we can discuss Bob’s actions. If he holds an Ace, he will always bet, as he holds the nuts and needs to get paid off, so betting dominates checking. What is he going to do with a King? Well, he can bet or check, but should he bet? To answer this question, we need to think about the reduced strategy of Alice who will always call with an Ace and never call with a Queen. Now that we know this, it should be clear that betting with a King accomplishes nothing, as Bob will always get called when he is beaten and never get called by a worse hand. He can lose less and win the same by simply checking. Checking dominates betting a King for Bob. What about a Queen? Both options remain valid. The reduced game can be seen in Figure 3.

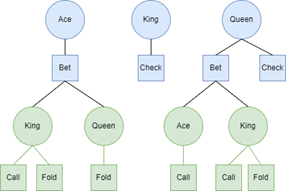
Now that we have reduced this game down to its simplest form, it’s worth taking a moment to show the payoff matrix of the reduced game. This can be seen in Table 1, which depicts the payoffs from Bob’s perspective.

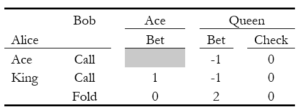
Let’s take a moment to intuitively discuss what is happening here. Bob has two sources of value: stealing pots with Queens and getting paid off with Aces. He has created a situation where the value of both options is equal, and there is nothing that Alice can do to prevent him from getting his value from this game. It’s important to understand that “value” in this context is the incremental value that Bob gains by employing a strategy, whatever that strategy happens to be. Alice is indifferent when Bob bets a Queen 1/3 of the time, because Bob’s game value is 1/18 if Alice calls 100% of the time or if Alice folds 100% of the time. In fact, his game value remains 1/18^th of a bet regardless of what Alice chooses to do. But she must call one in three times when she has a King to also avoid being exploited. If she employs this strategy, then it doesn’t matter what Bob does, as he can never do better than 1/18^th of a bet. Alice becomes indifferent to Bob’s strategy because no matter what Bob does – bluff at 100% frequency or 0% frequency  – his game value always remains at 1/18^th of a bet.

The AKQ game illustrates a fundamental aspect of poker strategy: bluffing is not merely a fun aspect of the game, it’s an essential tactic for winning. In our analysis, we see that Bob’s optimal strategy involves betting with both his strongest hands (Aces) and his weakest (Queens), while conserving hands with moderate strength (Kings) for “showdown value.” This creates what’s known as a “polarized” range, where Bob’s betting range is split between very strong and very weak hands. On the other side, Alice, facing Bob’s bets, must occasionally call with less than perfect hands (like Kings), and the frequency of these calls should be calibrated not based on Bob’s actions, but rather in relation to the pot size. The AKQ game thus serves as a microcosm of larger poker strategy, teaching players the importance of range balancing, bluffing, and the art of the call – skills that are essential for success at the poker table.

Much like Bob’s strategy in the AKQ game, where the focus is not on outmaneuvering the opponent at every turn but rather on establishing a balanced approach that remains robust regardless of the opponent’s moves, risk parity strategies in finance adopt a similar ethos. Instead of seeking to exploit market inefficiencies or predict short-term movements, these strategies aim for a balanced portfolio where risk is evenly distributed across various asset classes. This approach ensures that the investor’s success isn’t tethered to the performance of a single asset or market condition but is instead derived from a strategic equilibrium that holds steady in diverse market scenarios. In essence, just as a well-planned strategy in a game can lead to success regardless of the opponent’s actions, a well-structured risk parity portfolio aims to achieve consistent performance across various market environments.